In [1]:
%matplotlib inline
from __future__ import division
import numpy as np
import matplotlib
from datetime import datetime
#Using https://dtcooper.github.io/python-fitparse/ to parse the fit file
from fitparse import FitFile
#These two help parse the tcx files not needed if only doing fit files
from xml.dom.minidom import parse
import xml.dom.minidom
#Plotly used for interactive plots for comparison
from plotly.offline import download_plotlyjs, init_notebook_mode, plot, iplot
from plotly.graph_objs import Scatter, Figure, Layout
init_notebook_mode(connected=False)
In [2]:
#LOAD AN EXAMPLE FIT FILE
fit = '2018-03-11-020856-ELEMNT BBCD-22-12.fit'
#LOAD AN EXAMPLE TCX FILE
tcx = 'rob0-2020-05-12-gendarme-1-80858341.tcx'
Load and parse an example fit file¶
In [3]:
#LOAD FIT FILE AND PARSE
fit_watts = []
fit_time = []
fitfile = FitFile(fit)
# Get all data messages
count = 0
for record in fitfile.get_messages('record'):
# Process all records
for record_data in record:
if record_data.name == 'power' and record_data.value:
fit_watts.append(record_data.value)
elif record_data.name == 'power':
fit_watts.append(0)
#continue
if record_data.name == 'timestamp': fit_time.append(record_data.value)
trim = len(fit_time)-len(fit_watts)
if trim > 0:
fit_time = fit_time[:-trim]
t = (fit_time[-1]-fit_time[0]).seconds/3600.
In [4]:
# Define the basic constants / assumed values
g = 9.81 #gravity in m/s^2
m = 79.4 #rider + bike mass in kg
Crr = 0.005 #approximate rolling resistance
CdA = 0.324 #approximate CdA in m^2 - hands on hoods elbows bent
Rho = 1.225 #air density sea level STP
#Calculate the average power from the fit file
p = np.average(fit_watts)
#This calculates the steady state velocity in m/s and converts to MPH
n = (((((8*g**3*Crr**3*m**3+27*CdA*Rho*p**2)/(CdA*Rho))**0.5+p*5.196)/(Rho*CdA))**(1/3.0))**2*Rho*CdA-2*m*Crr*g
d = 3**0.5*Rho*CdA*(((8*g**3*Crr**3*m**3+27*CdA*Rho*p**2/(CdA*Rho))**0.5+p*5.196)/(Rho*CdA))**(1/3.0)
v = n/d*2.23694
In [5]:
print "Average Power {:0.1f} - Average Speed: {:.1f} mph - Time: {:.1f} hours - Distance: {:.1f} miles".format(p,v,t,(v*t))
In [6]:
g = 9.81 #gravity in m/s^2
m = 79.4 + 1 #rider + bike mass in kg with 1kg more representing the rotational intertia
Crr = 0.005 #approximate rolling resistance
CdA = 0.324 #approximate CdA in m^2 - hands on hoods elbows bent
Rho = 1.225 #air density sea level STP
dt=1 #time step from the fit/tcx files
Calculating the speed through forward integration¶
- Starting with a iniiial velocity of 0 mph
- Calculate the speed at the next time step using the equation below
- Update the initial velocity with the current velocity and repeat
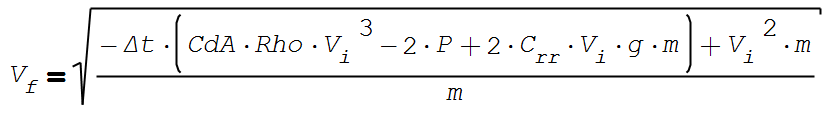
In [7]:
#This will calculate the speed at each time step
speed = [] #list to hold the second by second speed data
Vi = 0 #initialize the starting speed at 0
for p in fit_watts:
#for each time step do the following equation to determine the speed for the next second
Vf = ((-dt*(CdA*Rho*Vi**3-2*p+2*Crr*Vi*g*m)+Vi**2*m)/m)**.5
speed.append(Vf* 2.23694) ##convert from m/s to MPH for display, add this new speed to the list
Vi = Vf #update the current speed - it will be the start for the next calculation
v = np.average(speed) #get the average speed
t = (fit_time[-1]-fit_time[0]).seconds/3600. #calculate the length of the ride in hours
The next cell calculates the speed and distance using a steady state model and the average power - one step but less accurate¶
In [8]:
p = np.average(fit_watts)
n = (((((8*g**3*Crr**3*m**3+27*CdA*Rho*p**2)/(CdA*Rho))**0.5+p*5.196)/(Rho*CdA))**(1/3.0))**2*Rho*CdA-2*m*Crr*g
d = 3**0.5*Rho*CdA*(((8*g**3*Crr**3*m**3+27*CdA*Rho*p**2/(CdA*Rho))**0.5+p*5.196)/(Rho*CdA))**(1/3.0)
v_ss = n / d * 2.23694 #convert m/s to mph
In [9]:
#display the results for comparison
print "Power_Avg {:0.1f} - Speed_SS: {:0.1f} mph - Speed_Modeled {:0.1f} mph - Dist_SS: {:0.1f} miles - \
Dist_Modeled {:0.1f} miles".format(p,v_ss,v,(v_ss*t),(v*t))
Plot of the power (watts) and calculated speed (mph)¶
In [10]:
skip=1
iplot([{"x": fit_time[::skip], "y": fit_watts[::skip], "name": "power - watts"}])
iplot([{"x": fit_time[::skip], "y": speed[::skip], "name": "speed - mph"}])
Load and parse a tcx file¶
In [11]:
dom = xml.dom.minidom.parse(tcx)
file = dom.documentElement
tcx_watts = []
tcx_time = []
seg = dom.getElementsByTagName("ns3:Watts")
for c,item in enumerate(seg):
tcx_watts.append(int(item.firstChild.data))
seg = dom.getElementsByTagName("Time")
for item in seg:
t = item.firstChild.data
tcx_time.append(datetime.strptime(t, '%Y-%m-%dT%H:%M:%SZ'))
Calculating the speed through forward integration¶
- Starting with a initial velocity of 0 mph
- Calculate the speed at the next time step using the equation below
- Update the initial velocity with the current velocity and repeat
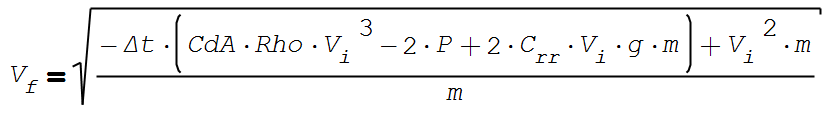
In [12]:
#This will calculate the speed at each time step
speed = [] #list to hold the second by second speed data
Vi = 0 #initialize the starting speed at 0
for p in tcx_watts:
#for each time step do the following equation to determine the speed for the next second
Vf = ((-dt*(CdA*Rho*Vi**3-2*p+2*Crr*Vi*g*m)+Vi**2*m)/m)**.5
speed.append(Vf* 2.23694) ##convert from m/s to MPH for display, add this new speed to the list
Vi = Vf #update the current speed - it will be the start for the next calculation
v = np.average(speed) #get the average speed
t = (tcx_time[-1]-tcx_time[0]).seconds/3600. #calculate the length of the ride in hours
The next cell calculates the speed and distance using a steady state model and the average power - one step but less accurate¶
In [13]:
#These next four lines show the calculation for the steady state velocity from the average power
p = np.average(tcx_watts) #calculate the average power
n = (((((8*g**3*Crr**3*m**3+27*CdA*Rho*p**2)/(CdA*Rho))**0.5+p*5.196)/(Rho*CdA))**(1/3.0))**2*Rho*CdA-2*m*Crr*g
d = 3**0.5*Rho*CdA*(((8*g**3*Crr**3*m**3+27*CdA*Rho*p**2/(CdA*Rho))**0.5+p*5.196)/(Rho*CdA))**(1/3.0)
v_ss = n / d * 2.23694 #convert the steady state velocity from m/s to MPH
In [14]:
#display the results for comparison
print "Power_Avg {:0.1f} - Speed_SS: {:0.1f} mph - Speed_Modeled {:0.1f} mph - Dist_SS: {:0.1f} miles - \
Dist_Modeled {:0.1f} miles".format(p,v_ss,v,(v_ss*t),(v*t))
Plot of Ride Power and Ride Speed¶
In [15]:
skip=1
iplot([{"x": tcx_time[::skip], "y": tcx_watts[::skip], "name": "power - watts"}])
iplot([{"x": tcx_time[::skip], "y": speed[::skip], "name": "speed - mph"}])
In [16]:
#This calculation is more explicit - however care must be taken when the speed is near zero
speed2 = []
Vi = 0
for p in tcx_watts:
Wroll = Crr*m*g*Vi #For each time step calculate Watts lost to rolling resistance
Wair = 1/2*CdA*Rho*Vi**3 #And the wind resistance
Wacc = p - Wroll - Wair #If this is positive then the bike accelerates, negative is slows down
if Vi: #This is to avoid a divide by 0 error if Vi = 0
F = Wacc/Vi #Calculate the force
else:
F = Wacc/1
a = F/m #Newton's second law - we get the acceleration
Vf = Vi + a*dt #This calculates how much velocity changes for this time step
speed2.append(Vf * 2.23694) #Record the speed for this time step
Vi = Vf #Update the current speed to be used in the next time step
This plot shows the results are the same¶
In [17]:
#This is a plot of the two methods - they line up as expected
iplot([{"x": tcx_time[::skip], "y": speed[::skip], "name": "method1"},
{"x": tcx_time[::skip], "y": speed2[::skip], "name": "method2"}])
In [ ]: